场景引入
假设有三台缓存服务器,编号分别为0、1、2,三台服务器用于缓存图片,现有三万张图片需要缓存,期望实现图片被均匀缓存到三台服务器,也就是大概每台服务器约存储1万张图片,以便能够均摊访问压力。如何实现?
哈希取模算法
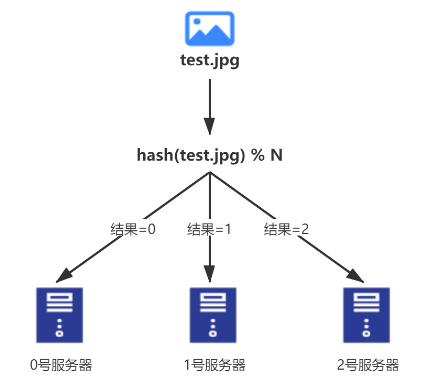
最直接的思路是对图片名称进行哈希,然后对得到的哈希值取模3,即 $hash(pic_name)%3$:
- 算法值最终得出图片缓存到哪个服务器
- 若到缓存服务器找不到,说明未缓存,尝试从数据库中找一找原文件的位置
新的场景
一段时间后,随着用户数据不断增加,这时图片缓存的数量平均每台已经增加到了一万五左右,于是决定对图片缓存集群进行扩容,还是按照一台一万左右的标准,预留一定空间,最终决定在原来的基础上,扩容3台服务器。
3分钟后扩容完成,后续10分钟内,生产环境大量缓存未命中告警,数据库压力飙升,最终数据库宕机,后端服务不可用。这就是缓存雪崩。
由于扩容后整个缓存集群增加到6台服务器,故哈希取模算法采用$hash(pic_name)%6$,这时问题就出来了,扩容之前哈希值计算为5的图片会从机器2取,扩容后会从机器5取,而刚扩容的机器还没有缓存图片,就会导致缓存未命中。显而易见,这里会有大约一半的缓存未命中。
这里存在的问题就是,当缓存集群节点数量发生变化时(无论是扩容、缩容,还是缓存节点宕机),哈希取模算法会导致大量缓存未命中,这个量级是与机器发生变动数量有关的。
那么如何解决该问题?
- 手动预热缓存:扩容时,先增加对应节点,但是不对外服务,然后手动把缓存数据写到新节点,然后再投入使用,由于实时性的问题,可能一些最新的数据不会被预热到新节点,但这个数量相比大量缓存未命中通常是可以接受的。不过该方案的问题在于,一是需要手动,二是若是缓存节点宕机场景就不起作用了,所以我们需要考虑自动切换的方案,还要尽可能减少缓存未命中的数量。
- 哈希一致性算法
- 哈希槽算法
哈希一致性算法
https://writings.sh/post/consistent-hashing-algorithms-part-2-consistent-hash-ring
哈希一致性算法通常也是基于取模,但能尽可能保证,哈希到某节点的图片在扩缩容节点后还能哈希到原本节点,这个比直接哈希取模会少很多哈希不到原本节点的情况。
基本思路如下:
- 哈希一致性算法采用$hash(pic_name)%2^{32}$,整个哈希空间为0到$2^{32}-1$,将整个哈希空间顺时针组织成一个环,称为哈希环
- 将集群中各个节点进行哈希,获得节点在哈希环中的位置,具体可以选择服务器的IP或主机名作为关键字进行哈希
- 对图片进行哈希,获得图片在哈希环中的位置,具体可以选择图片名称或者图片二进制内容为关键字进行哈希
- 从该图片在哈希环上的位置开始顺时针查找第一个集群节点位置,该集群节点就是图片应存放的位置
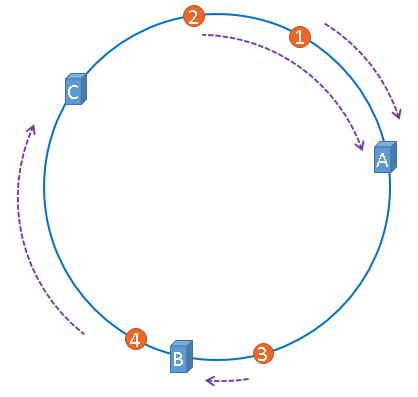
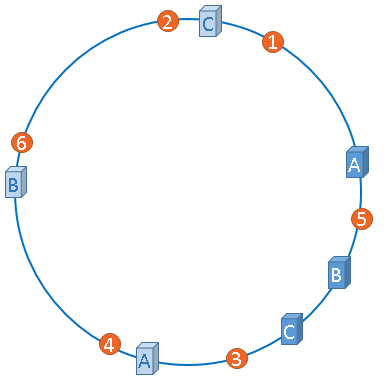
A、B、C分别为三台服务器在哈希环上的位置,1、2、3、4分别未四张图片,B宕机,A顺时针到B之前的所有数据需要迁移到C。
若假设哈希环上集群节点均匀分布,且图片均匀分布,那么假设上述节点B宕机,这时仅仅需要整体移动三分之一的数据即可。当有n个集群节点时,宕机任意一台只需整体移动n分之一的数据。对比一下哈希取余算法的未命中情况:
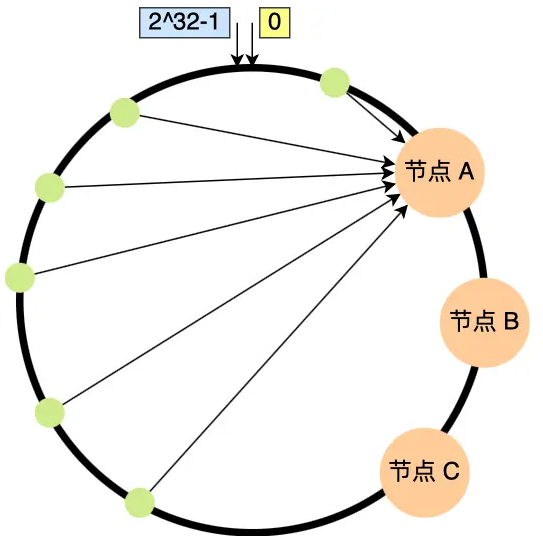
图中,蓝色部分表示集群节点数量,橙色部分表示hash(pic_name),假定初始节点数量为3,则绿色部分表示各图片哈希命中,红色部分表示从初始节点数量3扩容到对应节点数量时,缓存未命中的情况。可以看出,哈希取余算法会导致大量哈希未命中的情况,会导致命中率减低到一半及以下。

显然哈希一致性算法有很大的优势。不过,上述考虑的是集群节点均匀分布的情况,当图片比较少时,可能不会均匀分布,这没有什么问题,因为不会早成性能瓶颈,而当集群节点比较少时,可能不会均匀分布,这样就有问题了,同理,图片比较少没啥问题,图片多的时候,可近似认为图片均匀分布,但是节点不均匀分布,这样节点数据就会造成倾斜,即数据倾斜。这样会造成某一节点远大于其他节点,既不能充分利用各节点性能还容易造成瓶颈。
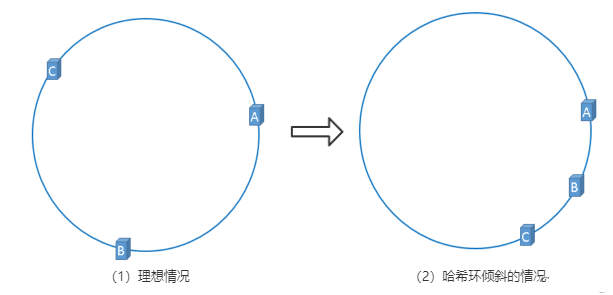
哈希一致性算法引入虚拟节点解决这个问题。
为了解决这种数据倾斜问题,一致性哈希算法引入了虚拟节点机制,即对每一个服务节点计算多个哈希,每个计算结果位置都放置一个此服务节点,称为虚拟节点,一个实际物理节点可以对应多个虚拟节点,虚拟节点越多,hash环上的节点就越多,缓存被均匀分布的概率就越大,hash环倾斜所带来的影响就越小,同时数据定位算法不变,只是多了一步虚拟节点到实际节点的映射。具体做法可以在服务器ip或主机名的后面增加编号来实现,加入虚拟节点以后的hash环如下:
实际节点+虚拟节点越多,越不容易造成倾斜。当然实虚节点之和越多,哈希一致性算法时间复杂度和空间复杂度越高。假设实虚节点之和为n,设其为一个长度为n的数组,则定位一张图片具体节点复杂度为:
- 时间复杂度:$O(log_2n)$。由于是有序的,整体可采用二分查找。
- 空间复杂度:$O(n)$。保存n个有序节点。
另外,虚拟节点的引入使得加权节点成为了可能,比如A节点性能很高,可以让A节点虚拟节点更多一点。
哈希槽算法
Redis中哈希槽$2^{14}=16384$